Module 3 Section 2- Binary negative numbers

When people write a negative number, they usually write a minus sign first, followed by the number's magnitude. The magnitude is the absolute value of the number. The preceding minus sign tells us it is a negative number. If the minus sign is missing, then we know the number is non-negative. (We do not say it must be positive, because it could be zero. Zero is neither positive nor negative. Zero is not written with a minus sign.)

Harken back to when we were talking about a single bit being able to represent a "TRUE" or "FALSE" piece of information (such as whether a customer did or didn't want raisin's in their bread pudding). We can do the same trick here. Let's use a bit to represent whether a number is negative or non-negative.We'll sacrifice one of the bits in our bit field to be a sign bit. If the sign bit is '1' then the number is negative. If the sign bit is '0' then the number is non-negative. The remaining bits will tell us the magnitude of the number.

Which bit should we sacrifice to be the sign bit? Well, since people write the minus sign to the left of the number, we should probably sacrifice the most significant (leftmost) bit.

So let's try out this new representation for negative binary numbers using a 4-bit field. Here it is:

How would we represent, say, a -3? Well, since there is a minus sign, the sign bit would be set to "TRUE" or '1'. The magnitude is '3', which in binary is '11B'. So, the final bit pattern for representing -3 would be:

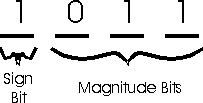
What about a positive 6? Well, there's no minus sign, so the sign bit is '0'. The magnitude bits would be '110', and we would have:

What is the most negative number we can represent? It would have the minus bit set to '1' and the large possible magnitude, which is '111B'. So, -7 is the most negative number we can represent with a 4-bit field. What about the most postive? That would a positive 7.

In general, when you use this representation with an n-bit field, the range of numbers that can be represented is:

So far everything looks pretty good, but closer inspection shows some serious problems with this representation, which we call signed magnitude representation. Here is a number line which shows all the numbers that can be represented with a 4-bit signed magnitude number.

Problem #1 with signed magnitude - "The Case of the Missing Bit Pattern" : How many possible bit patterns can be created with 4 bits? Easy, we know that's 2⁴, or 16. In unsigned representation, we were able to represent 16 numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, and 15. But with signed magnitude, we are only able to represent 15 numbers: -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, and 7. There's still 16 bit patterns, but one of them is either not being used or is duplicating a number. That bit pattern is '1000B'. When we interpret this pattern, we get '-0' which is both nonsensical (negative zero? come on!) and redundant (we already have '0000B' to represent 0).

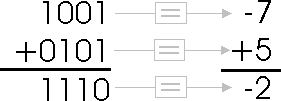
Problem #2 with signed magnitude - "Requires Special Care and Feeding": Remember we wanted to have negative binary numbers so we could use our binary addition algorithm to simulate binary subtraction. How does signed magnitude fare with addition? To test it, let's try subtracting 2 from 5 by adding 5 and -2. A positive 5 would be represented with the bit pattern '0101B' and -2 with '1010B'. Let's add these two numbers and see what the result is:

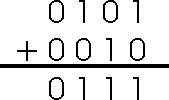
Now we interpret the result as a signed magnitude number. The sign is '0' (non-negative) and the magnitude is '7'. So the answer is a postive 7. But, wait a minute, 5-2=3! This obviously didn't work. Conclusion: signed magnitude doesn't work with regular binary addition algorithms.

Signed magnitude has more disadvantages than it does advantages.

ADVANTAGE of signed magnitude: You can determine whether a number is negative or non negative simply by testing the most significant bit.

DISADVANTAGES of signed magnitude: One of the bit patterns is wasted. Addition doesn't work the way we want it to.

First, let's draw a number line which shows positive and negative integers about 0. Again, we will limit ourselves (for right now) to a 4-bit field. Let's keep the bit patterns that represent 0 through 7 since they all meet our requirements (sign bit is easy to test and addition works). Now observe the bit pattern for '0' which is '0000B'. We need a bit pattern to represent -1. In order for this bit pattern to work with addition, then when we add '0001B' to it, we should get '0000B'. What bit pattern, when '0001B' is added to it yields '0000B'?

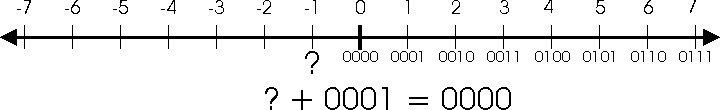
The answer to this question may not be immediately obvious, until you remember that we have limited ourselves to a 4-bit field. Consider the bit pattern '1111B'. Add it to '0001B'

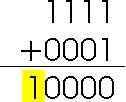
The result is '10000B'. But since we have limited ourselves to 4-bits, the '1' (in the colored box) is ignored, or "dropped." The remaining 4-bits are the answer, 0. Therefore, '-1' can be represented by '1111B'. It meets all of our requirements: the most significant bit tells us the sign of the number, and it works with addition. Likewise, we should be able to find a bit pattern for '-2' by asking the question 'What bit pattern added to '0001B' gives us '1111B' (-1)? The answer, as you know, is '1110B'. Here is a new number line which shows this numbering scheme.

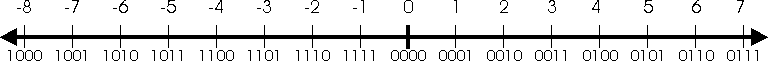
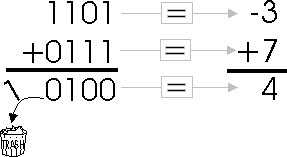
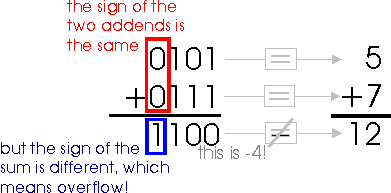
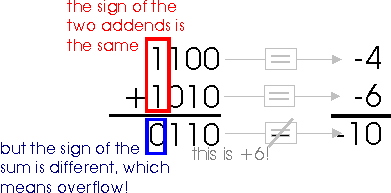
With this representation, known as two's complement, we can represent the negative numbers from -8 to -1, whereas with signed magnitude we could only represent -7 to -1. You can see that the bit pattern which used to represent '-0' (whatever that is) has been used to extend the negative range. Also, all negative numbers have the most significant bit set to '1'. What about addition? Does it work with the "regular" binary addition algorithm? The answer is 'yes.' However, there are some limitations of which we must be aware.

• Once you have chosen a bit-field width, you must stay with it! Our examples have used a 4-bit field. Whenever we have stored a binary number, we have always expressed them in 4-bits, with leading zero's if necessary. When doing addition which resulted in more than 4 bits, we threw the 5th bit (most significant bit) away. There are ways to convert to large width fields (see below).
• Addition of any negative number with a non-negative number will always produce the correct result. If you add a negative number with any non-negative number you will always get the correct answer. Here are a few examples:

 


 
 



• Care must be taken when adding numbers of like sign since overflow can occur. If you add two numbers of like sign and the result is of the opposite sign, then the result cannot be used. This "overflow" condition occurs because, in order to represent the result, we would need more bits than are available in the bit field. (Remember, we can't just "enlarge" the size of the result- it must remain the same size as the operands.) Here are examples for adding two negative numbers, and adding two positive numbers, each of which results in overflow.


 



• You can enlarge the size of the bit field, but only before you perform any operations, and it must be done a certain way. If you find that the size of the bit field is too small and overflow is occuring, you can promote the values to larger bit fields. This is done by a technique called sign extension. To enlarge the bit field, add bits on the left, duplicating the most signficant bit.  This preserves the sign of the number and does not alter its value. Remember, you must promote all values to the same size. The table below illustrates sign-extension of a 4-bit number to 5, 6, and 8-bit fields. In each case, the most significant bit of the original 4-bit field (in blue) is simply repeated as many times as necessary on the left(in red).

Original 4-bit Value	Extended to 5-bits	Extended to 6-bits	Extended to 8-bits
0010	00010	000010	00000010
1000	11000	111000	11111000

 

Homework Questions

Write these decimal numbers as 8-bit 2's complement:
1. 12
2. -20
3. -128
4. 127
5. 0
   
   For each signed-decimal addition below, first do the decimal addition and show the result. Next, convert the operands to 8-bit 2's complement binary and perform binary addition on them. Convert the result of the binary addition to decimal and compare it with the result of the decimal addition.
6. 14 + 20
7. 45 - 45
8. -12 + 22
9. 120 - 20
10. 32 + -5
    
    Which of the following decimal additions will cause overflow to occur if 8-bit binary two's complement is used?
11. 4 + 120
12. 70 + 80
13. 100 - 60
14. -100 - 27
15. 100 + 100
    
    Sign-extend each of the following 4-bit binary numbers to 8 bits.
16. 1011
17. 0101
18. 0000
    
    What is the range of numbers that can be represented with signed magnitude and two's complement for the following number of bits?
19. 6
20. 17