------------------------------------------------------------------------------
MC logo
Peg Jump Puzzle
[^] Prolog Examples
------------------------------------------------------------------------------
<<Trains Schedule Puzzle jump2.pl Simple (Slow) Sort>>
% Form of board, x for full, o for vacant spaces.  Starting is
% [ [o], [x, x], [x, x, x], [x, x, x, x] ]

% Legal jumps along a line.
linjmp([x, x, o | T], [o, o, x | T]).
linjmp([o, x, x | T], [x, o, o | T]).
linjmp([H|T1], [H|T2]) :- linjmp(T1,T2).

% Rotate the board
rotate([ [A], [B, C], [D, E, F], [G, H, I, J], [K, L, M, N, O]],
        [ [K], [L, G], [M, H, D], [N, I, E, B], [O, J, F, C, A]]).

% A jump on some line.
horizjmp([A|T],[B|T]) :- linjmp(A,B).
horizjmp([H|T1],[H|T2]) :- horizjmp(T1,T2).

% One legal jump.
jump(B,A) :- horizjmp(B,A).
jump(B,A) :- rotate(B,BR), horizjmp(BR,BRJ), rotate(A,BRJ).
jump(B,A) :- rotate(BR,B), horizjmp(BR,BRJ), rotate(BRJ,A).

% Series of legal boards.
series(From, To, [From, To]) :- jump(From, To).
series(From, To, [From, By | Rest])
        :- jump(From, By), 
           series(By, To, [By | Rest]).

% Print a series of boards.  This puts one board per line and looks a lot
% nicer than the jumble that appears when the system simply beltches out
% a list of boards.  The write_ln predicate is a built-in which always
% succeeds (is always satisfied), but prints as a side-effect.  Therefore
% print_series(Z) will succeed with any list, and the members of the list
% will be printed, one per line, as a side-effect of that success.
print_series_r([]) :- 
    write_ln('*******************************************************').
print_series_r([X|Y]) :- write_ln(X), print_series_r(Y).
print_series(Z) :- 
    write_ln('\n*******************************************************'),
    print_series_r(Z).

% A solution.
solution(L) :- series([[o], [x, x], [x, x, x], [x, x, x, x], [x, x, x, x, x]],
                   [[x], [o, o], [o, o, o], [o, o, o, o], [o, o, o, o, o]], L).

% Find a print the first solution.  
solve :- solution(X), print_series(X).

% Find all the solutions.
solveall :- solve, fail.

% This finds each solution with stepping.
solvestep(Z) :- Z = next, solution(X), print_series(X).
Most of the code is concerned with defining a legal move. First, we define horizontal moves.
The two legal changes (left and right jumps) are expressed in the two basis rules for linjmp:
linjmp([x, x, o | T], [o, o, x | T]).
linjmp([o, x, x | T], [x, o, o | T]).
These define the horizontal jump, including the requirement that the pegs to the right are unchanged (the contents of T).

The left part of the row is kept the same by the recursive part of linjmp:

linjmp([H|T1], [H|T2]) :- linjmp(T1,T2).
The left part of the row is filled with H) on each side.

Now, the basis case of horizjmp

horizjmp([A|T],[B|T]) :- linjmp(A,B).
makes sure the rows after the change are the same, and the recursive case of horizjmp
horizjmp([H|T1],[H|T2]) :- horizjmp(T1,T2).
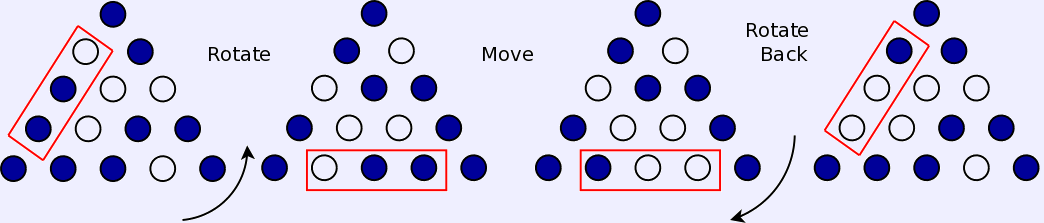
makes sure the rows before are all unchanged.

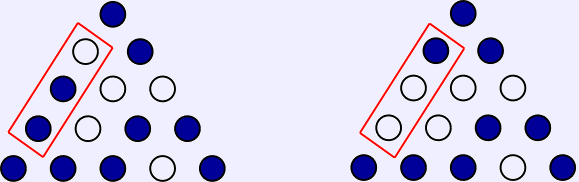
Once the horizontal jumps are taken care of, the other jumps are done by using rotation to turn them into horizontal jumps. For instance, the move:

is handled as:
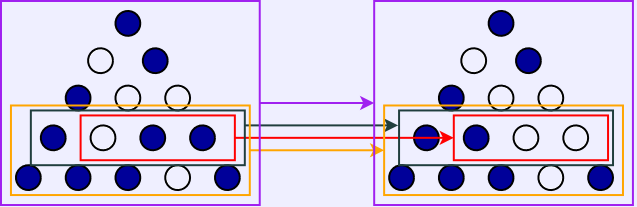
The rotate rule handles rotating the board (either way), and jump puts it all together to define all legal jumps.
<<Trains Schedule Puzzle Simple (Slow) Sort>>