75 pts |
Circuit Try |
Due: April 6 |
Create two classes using the posted circuit simulation examples.
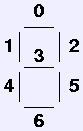 The first one simulates a the common seven-segment display that looks
like a squared-off 8. The device take seven input connections, each
controlling one segment. Each segment is turned on or off by the value
of one input bit, numbered from the right, as shown in figure. You can
simulate this in text by using the underscore character for the horizontal
lines, and the vertical bar character for the verticals. For instance,
the simple test program:
The first one simulates a the common seven-segment display that looks
like a squared-off 8. The device take seven input connections, each
controlling one segment. Each segment is turned on or off by the value
of one input bit, numbered from the right, as shown in figure. You can
simulate this in text by using the underscore character for the horizontal
lines, and the vertical bar character for the verticals. For instance,
the simple test program:
require "segdisp"
sb = SwitchBank.new
ss = SevenSeg.new
7.times { sb.join(ss) }
sb.value = 0x57
sb.value = 0x6d
Produces the output
_
| |
|_
_
_|
_|
The first form is produced by hex 57, which, in binary is 101 0111. Compare
this to the diagram to see that the segments where one bits appear
(0, 1, 2, 4 and 6) are displayed, while the others are not. Likewise, the 3
form is produced by hex 6d, which is 110 1101 in binary. You should
implement this in Ruby using the class name
SevenSeg. Derive your class
from
NumberOut or one if its descendents.
The second thing you need to create is a decoder so that a four-bit number
may be properly shown on the seven-segment display. This unit has four
inputs for the number to display, and seven outputs for the seven
display inputs. You should create it using gates, and construct class
Decoder derived from Blueprint. Here's a small driver:
require "segdisp"
require "decode"
bp = Decoder.new
sb = SwitchBank.new
dc = bp.another
ss = SevenSeg.new
NumberOut.shush
7.times { dc.join(ss) }
4.times { sb.join(dc) }
NumberOut.shush(false)
sb.value = 4
sb.value = 9
sb.value = 12
And its output
|_|
|
_
|_|
_|
_
|
|_
The number goes into the decoder, and it produces the right signals
to display it and the seven-segment device. For inputs over nine, the
decoder produces a representation of the hex digit. Here are all the
forms:
_ _ _ _ _ _ _ _ _ _ _ _
| | | _| _| |_| |_ |_ | |_| |_| |_| |_ | _| |_ |_
|_| | |_ _| | _| |_| | |_| _| | | |_| |_ |_| |_ |
To get these, you must decide, for each four-bit input, whether each
sigment should be lighted or not. For each segment (each output bit),
you produce a boolean expression of the input bits which determines
the if the segment is on (the value of the output bit). You must then
construct this expression using the gate classes from the simulation.
I've given some boolean expressions below which you may use;
you'll still have to
build the simulated gate circuits.
Segment Expressions
Below are expressions for each of the seven segment output values in
terms of the four input values. Input bits are numbered from the right,
as usual. Setting the terms adjacent means "and," the plus sign
means "or" and ¬ means "not".
s0 = i1 (¬i3) + i1 i2 + (¬i0) i1 + (¬i0) i3 + (¬i0) (¬i2) + i0 i2 (¬i3) + (¬i1) (¬i2) i3
s1 = i1 i3 + (¬i2) i3 + (¬i0) i2 + (¬i0) (¬i1) (¬i2) + (¬i1) i2 (¬i3)
s2 = (¬i2) (¬i3) + (¬i1) (¬i2) + (¬i0) (¬i1) (¬i3) + i0 i1 (¬i3) + i0 (¬i1) i3 + (¬i0) (¬i2)
s3 = (¬i0) i1 + (¬i2) i3 + i1 i3 + i1 (¬i2) + (¬i1) i2 (¬i3) + i0 (¬i1) i2
s4 = i2 i3 + i1 i3 + (¬i0) i1 + (¬i0) (¬i2)
s5 = i2 (¬i3) + (¬i2) i3 + i0 (¬i1) + (¬i1) (¬i3) + i0 (¬i3)
s6 = (¬i1) i3 + (¬i0) (¬i2) (¬i3) + i0 i1 (¬i2) + (¬i0) i1 i2 + i0 (¬i1) i2
Submission
When your program works, is well-commented, and properly
indented,
submit it
here.
 The first one simulates a the common seven-segment display that looks
like a squared-off 8. The device take seven input connections, each
controlling one segment. Each segment is turned on or off by the value
of one input bit, numbered from the right, as shown in figure. You can
simulate this in text by using the underscore character for the horizontal
lines, and the vertical bar character for the verticals. For instance,
the simple test program:
The first one simulates a the common seven-segment display that looks
like a squared-off 8. The device take seven input connections, each
controlling one segment. Each segment is turned on or off by the value
of one input bit, numbered from the right, as shown in figure. You can
simulate this in text by using the underscore character for the horizontal
lines, and the vertical bar character for the verticals. For instance,
the simple test program: