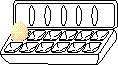








Binary means base 2(note the prefix bi). Base 2 (binary) has 2 digits: 0, 1. Since binary numbers are made up of binary digits, we often call a binary digit a bit (short for binary digit). We may also refer to a place value position as a bit. In other words, the binary number '1010' requires 4 bits to write, and those bits are '1', '0', '1' and '0'.
For any number system that has a base b, the first b non-negative numbers are represented by the digits themselves. For base b=2 (binary), the first 2 numbers are 0 and 1.
Counting in binary is just like counting in decimal, except that you
run out of digits much more quickly and have to resort to more value places
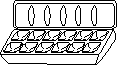
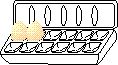
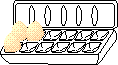
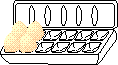
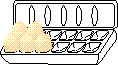
sooner. To count the number of eggs in a dozen in binary would be as follows:
0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100. The following
table will show how this sequence looks in both binary and decimal, so
you can compare them.
| Eggs | In Decimal | In Binary | Comments |
 |
|
|
|
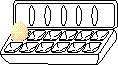 |
|
|
So far, the sequences are exactly the same |
 |
|
|
Here, binary has run out of digits and must resort to another place, whereas decimal still has more digits to use. |
 |
|
|
|
 |
|
|
Again, binary has run out of digits in the 2's place, and must expand to the 4's place. Decimal still has not exhausted it's 1's place. |
 |
|
|
|
 |
|
|
|
 |
|
|
|
 |
|
|
|
 |
|
|
|
 |
|
|
Finally, decimal must resort to a second value place, then 10's. |
 |
|
|
|
 |
|
|
First, let's understand what the word digital means. The counterpart to digital is analog. You can understand the difference by thinking about a clock...well, two clocks. Here they are:
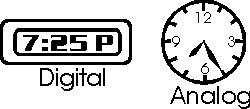
The digital clock is capable of representing a finite amount of information. It can tell us the time by showing use 1 of 12 possible hours, 1 of 60 possible minutes, and either AM or PM. There's no way for the digital clock to show us how much of the minute has passed. Even if you added two more digits for seconds, you wouldn't be able to tell how far between seconds you are. And even if you added more digits for that, the actual time could always be "between" two possible times the digital clock can show. You would have to have an infinite number of digits in the display to be able to tell exactly what time it was using the digital clock. Of course, that's not practical! Digital can mean descrete, as it does in this example. That means that there is a finite number of things the clock can show, even though the thing it represents (the current time) could have an infinite number of actual values.
The analog clock is able to show an infinite number of values, because the hands sweep through a continuous domain. In other words, when the time is actually between two minutes, the hand will be positioned halfway between two minutes on the face of the analog clock. Digital computers (such as the digital clock) often have to represent analog information, and do so by choosing the closest discrete value to the continuous value. For example, if the time is actually 4:03:12PM, then our digital clock would either show 4:03PM or 4:04PM.
The simplest discrete domain to work with, and the one that modern digital computers work with, has only two values. These values are known by several names. 'OFF' and 'ON', 'NO' and 'YES', 'FALSE' and 'TRUE', and (you guessed it) '0' and '1'. The reason computers use binary is because the values '0' and '1' can be represented by electricity. If there is electrical current on a wire, we'll say that wire is signalling a '1'. If there is no electrical current on a wire, then we'll say it is signalling a '0'.
Computer engineers are experimenting with computers that use more than two values, but they are not yet practical. These computers would use different levels of eletrical current to represent more discrete values. For example, no current could be '0', medium current could be '1', and high current could be '2' - which would give you a trinary computer. For our studies, however, we will constrain ourselves to the binary computer. It's simple, and it is the current technology.
We should be able to apply expanded notation to binary numbers. For example, the binary number '10110' written in expanded notation would be:
Notice that everything is written in binary. You would read it as "1 times 2 to the 4th plus 0 times 2 to the 3rd plus 1 times 2 to the 2nd plus 1 time 2 to the 1st plus 0 times 2 to the 0." However, we are going to use expanded notation as a tool for converting binary to decimal. So let's rewrite the expanded notation as a decimal expression:
Now, by actually carrying out a computation, we can condense this to a base 10 (decimal) number which is equivalent to the binary '10110'. Remember, they are the same number, just written differently. So the above becomes:
So, '10110' in binary is the same as '22' in decimal.
Another observation you may have made is that anytime a '0' is in a bit position, it will never contribute anything but zero to the sum. So, if we are going to convert binary to decimal this way, we can save a lot of time by just not writing down the '0' bits to begin with. For example, let's convert the binary number '10010' to decimal, and remember that '0' doesn't contribute to the sum. We get:
And another observation now is that the '1' bits always contribute exactly that power of two. In other words, you waste time doing the multiplication. All you have to do is write a series of powers of two as a sum. For example, let's convert the binary number '1011011' keeping this in mind:
Fractions also work, just as with decimal numbers. Negative exponents are used to denote negative powers of two. Instead of a "decimal" point we now have a "binary" point. The place value of the postion to the right of the binary point is 2-1, or one-helf. Next is 2-2, or one-fourth. So what is the binary number '100.101' in decimal? First, write the expanded notation:
Write the following binary numbers in expanded notation, including all information even if it is redundant:
Convert the above numbers (listed again below) to decimal using the expanded notation as an intermediate form.