CSC110 - Computer Mathematics

Module 1 Section 3- Properties of Binary Numbers

As we have learned, binary numbers are used by modern digital computer systems because they are very simple. Each digit is one of two values: '0' or '1'. A single bit by itself can be useful, by representing 'FALSE' and 'TRUE' - a flag. For example, a single bit of storage could store '0' (FALSE) if a customer does NOT want raisins in their bread pudding, or '1' (TRUE) if they do. Applications of a single bit are pretty much limited to this kind of TRUE/FALSE use. The real power of the bit comes into play when we group several together.

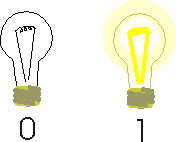
Let's use light bulbs to represent when a wire in the computer is carrying electrical current (the bulb is lit) and when it is not (the bulb is dark). A lit bulb means '1' and a dark bulb means '0', like this:

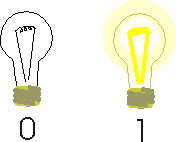
A computer with one bulb can represent two values, '0' and '1'. We could choose to interpret these values as 'FALSE' and 'TRUE' as we discussed earlier. Suppose a computer had two light bulbs to work with. What could we do with that? What are all the possible combinations of on and off? The table below shows them, and binary numbers that go with them.
 

Light Bulbs Binary Number Represented
00
01
10
11
As you can see, the way to list all possible combinations of on/off lights when there are two lights is to count all binary numbers that will fit into a two-bit field. So, for two lights (two bits) there are four possible combinations - twice as many as we had with one bit (we had only two combinations with just one bit). The binary numbers we counted were from 0 to 3.

In fact every time we add a light, we double the number of combinations. With 3 light bulbs, we get 8 combinations representing the numbers from 0 to 7.. With 4 light bulbs, 16 combinations representing the numbers 0 to 15. There is a definite pattern here, and it is important to remember it.

For any bit field of width n the following is true:

So, for a 7-bit field, we know that the total number of combinations we can represent with that field is 27, or 128, and that the range of numbers we can represent is 0 up to 27-1, or 127.

Historically, bits have been grouped together in groups of 8. An 8-bit field is called a byte. A byte can represent 256 different bit patterns, which is a number range from 0 to 255.

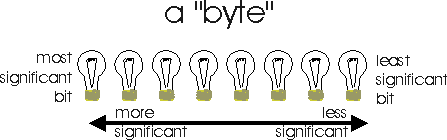
Now that we are working with larger bit fields, we need to learn some more terminology. Each bit in the bit field has a different significance. That is, some bits contribute more to the number being represented than others. Think about it. Which makes the biggest difference: a '1' appearing in the 2's place, or in the 8's place? The 8's place, of course! A one appearing in the 8's place adds 8 to the total number, which is more significant than adding just 2.

The rule is that bits on the left are more significant than bits on the right. We call the left-most bit the most significant bit or the high bit. We call the right-most bit the least significant bit or the low bit. If one bit is to the left of another, we say the first bit is more significant than the second, or that the second is less significant than the first.

Homework Questions

    Create a table that lists all the possible bit patterns and the equivalent decimal numbers for the following.

  1. a 1-bit field
  2. a 2-bit field
  3. a 3-bit field
  4. a 4-bit field
  5. a 5-bit field

    How many bit patterns are there, and what is the range of numbers that can be represented with the following?

  6. a 1-bit field
  7. a 2-bit field
  8. a 3-bit field
  9. a 4-bit field
  10. a 5-bit field
  11. a 6-bit field
  12. a 7-bit field
  13. a 8-bit field
  14. a 9-bit field
  15. a 10-bit field
  16. a 16-bit field
  17. a 20-bit field
  18. a 24-bit field
  19. a 30-bit field
  20. a 32-bit field
Next Module: Binary/Octal/Decimal/Hexadecimal Conversion
Previous Section: Introducing the Binary Number System
Return to Module Index