Module 2 Section 1 - Decimal to Binary Conversion

An obvious approach to solving this problem is to do a 'reverse' of the binary-to-decimal algorithm. We call this the inspection method. First, find the largest power of 2 which is less than or equal to the number you are converting. Write down that power of two and subtract it from the number. Keep doing this until the number is 0. When you're done, you know what bit positions will require a '1' bit in the new binary number.

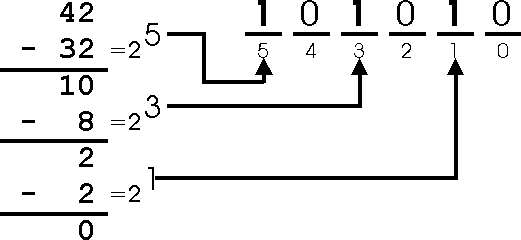
For example, let's convert decimal 42 to its binary representation. The largest power of 2 that is less than or equal to 42 is 2⁵. We write down '5' and substract 2⁵ (32) from 42. The number has been reduced to 10. The largest power of 2 that is less than or equal to 10 is 2³. We write down '3' and substract 2³ (8) from 10. The number has been reduced to 2. The largest power of 2 that is less than or equal to 2 is 2¹. We write down a '1' and substract 2¹ (2) from 2. The number has now been reduced to 0, and we stop. We wrote down '5', '3', and '1'. That means that the binary number has 6 bit positions, with positions 5, 3 and 1 having a '1' in them, and the rest '0'. Therefore, '101010' is the binary equivalent of decimal 42. Here's a graphic representation of this example:

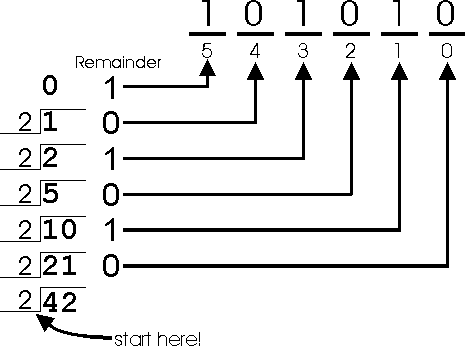
This method is easy to understand because it is a direct result of what we know about expanded notation. However, there is another way to convert decimal numbers to binary numbers that some people find easier, called the division method. Again, start with the decimal number you wish to convert. Divide this number by 2 and write the remainder (which will always be either 0 or 1) down. Divide the number by two again, and write the new remainder to the left of the last remainder. Continue doing this until the number is zero. So, for the number 42, when we divide 42 by 2 we get 21 with a 0 remainder, and write down '0'. Divide 21 by 2, and we get 10 with a 1 remainder, which we write down as '10'. Divide 10 by 2 and we get 5 with a 0 remainder, which we write down as '010'. Divide 5 by 2 and we get 2 with a 1 remainder, which write down as '1010'. Divide 2 by 2 and we get 1 with a 0 remainder, which write down as '01010'. Divide 1 by 2 and we get 0 with a 1 remainder, which we write as '101010'. The number is 0, so we stop, and the answer is the string of remainders we wrote down '101010'. Here is a graphic representation of this example:

Convert these numbers to binary using the inspection method. Show all work.

1. 12
2. 20
3. 101
4. 32
5. 33
6. 15
7. 248
8. 255
9. 256
10. 1000

    Convert these numbers to binary using the division method. Show all work.

11. 14
12. 17
13. 119
14. 64
15. 65
16. 31
17. 60
18. 63
19. 99
20. 10732