Module 2 Section 2- Octal and Hexadecimal Number Systems

• FACT: Computers use binary numbers for storage and computation.
• FACT: Binary numbers take up many digit positions to store even small numbers
• FACT: Binary numbers are hard for people to work with because they are so long and repetitive
• FACT: Humans work better with number systems of higher bases, especially base 10
• FACT: Converting decimal to binary is tedious, at best
• QUESTION: How can humans ever hope to work easily with low-level computer data?

The biggest gripe people have about binary is that it takes so many bit positions to represent even the small numbers. And the biggest gripe people have about decimal is that it is so difficult to convert to binary. The best of both worlds would be to choose a radix which offers a more compact representation of numbers, and is easy to convert to binary. The octal number system, which has a base of 8, is such a system.

Since octal uses base 8, there are 8 digits: 0, 1, 2, 3, 4, 5, 6, 7. the following table shows the first 16 numbers in decimal, binary, and octal.
 

Binary	Octal	Decimal
0000	00	0
0001	01	1
0010	02	2
0011	03	3
0100	04	4
0101	05	5
0110	06	6
0111	07	7
1000	10	8
1001	11	9
1010	12	10
1011	13	11
1100	14	12
1101	15	13
1110	16	14
1111	17	15

As you can see, the octal number system is much more efficient with space than binary, though not quite as efficient as the decimal system. Therefore, it fulfills one of our requirements: that numbers take up less space. But what about ease of conversion? Is octal easier to convert to binary than decimal?

Certainly, we could use our regular conversion methods to convert octal to decimal. We could successively subtract the largest power of 8, or successively divide by 8, as we learned in the last section. But a simple observation about the table above will reveal an easier method. Here is a hint: whenever there is a carry from the one's position to the eight's position in the octal number, there is also a carry from the 4's position to the 8's position in the binary number. Here's another hint. suppose we "gray out" the 8's position in both the binary and octal columns, then compare the numbers left over. Maybe you will see it then...
 

Binary	Octal
0000	00
0001	01
0010	02
0011	03
0100	04
0101	05
0110	06
0111	07
1000	10
1001	11
1010	12
1011	13
1100	14
1101	15
1110	16
1111	17

The same sequence of 8 number repeats twice. As the binary counts from '000' to '111', the octal counts from '0' to '7'. After '111'/'7', they both "roll over" to '000'/'0'. In fact, every three bits of a binary number line up exactly with every octal digit of the octal number. This is due to the fact that 8 is itself a power of 2. It also means that conversion of binary to octal and octal to binary requires remembering only 8 conversions: how to convert any 3-bit binary number to it's 1-digit octal counterpart.

Converting binary to octal: Counting from right to left, draw a line between every group of 3-bits. The most significant group may not have exactly three bits, so you can just pretend the others are zeros. Now convert each group of three to a single, octal digit. The conversion of a 3-bit number to an octal number is easy. You can memorize the patterns easily and, even if you forget, they are not hard to figure out. The resulting octal digits, when written together in the same order, are the equivalent binary number. Here's an example which converts the binary number '11111010' to its equivalent octal number.

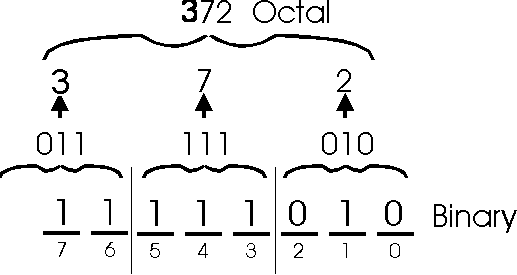
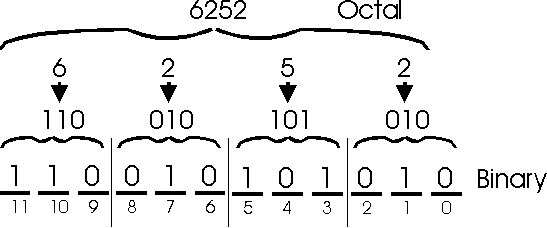
Converting octal to binary: This is simply the reverse of the above process. For every octal digit, just write down the 3-bit pattern that represents it. Here is an example which converts octal number 6252 to binary.

Great! Except there is one slight annoying problem. Remember that modern computers like to group bits together into bytes, so we're going to be working with bytes an awful lot, so we need to be sure that octal is a good idea for use with bytes before we go with it. Let's see how an 8-bit field lines up with our octal conversion.

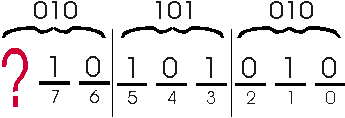
As you can see, for any byte we try to represent, the most-significant octal digit will never exceed the value '3'. Since a byte is 8 bits, and octal digits each represent 3-bits, the third octal digit will never be asked to represent more than 2 bits.  That's wasted space, and we don't like wasted space.

So, we now add a third requirement to our list. Here's the list of requirements we want for our new numbering system:

• Must make efficient use of space
• Must be easy to convert between binary
• Must be as efficient as possible when representing bytes

Since this is base 16, there will be 16 digits. Let's count them. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ...umm, uh oh.

This is the first base we've encountered that is greater than ten, and we're used to using only 10 digits: 0 through 9. However, we need 6 more to have a full set of hexadecimal digits. It may sound strange, but we will use letters for our other six digits. A, B, C, D, E and F. So, the full list of hexadecimal digits is: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. The hexadecimal digit A is the number 10 in decimal. The hexadecimal digit F is number 15 in decimal. We now show the table of the first 16 non-negative numbers, with a column added for hexadecimal.
 

Binary	Octal	Decimal	Hexadecimal
0000	00	0	0
0001	01	1	1
0010	02	2	2
0011	03	3	3
0100	04	4	4
0101	05	5	5
0110	06	6	6
0111	07	7	7
1000	10	8	8
1001	11	9	9
1010	12	10	A
1011	13	11	B
1100	14	12	C
1101	15	13	D
1110	16	14	E
1111	17	15	F

Hexadecimal is very efficient with space. It can count up to 15 before needing another place value position. Other properties of hexadecimal:

• It "lines up" with 4-bits in a binary field the same way an octal digit "lines up" with 3-bits. That means conversion will only be a matter of remembering the 16 hexadecimal digits and their associated 4-bit binary patterns.
• Since a hex digit can represent exactly 4-bits, two hex digits can represent exactly 8-bits (a byte). In other words: every byte has a 2-digit hexadecimal representation, and every 2-digit hexadecimal representation has a corresponding byte representation.

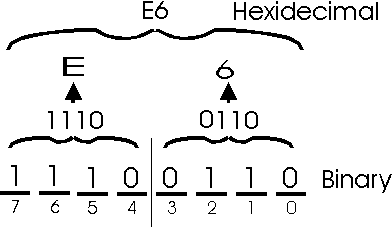
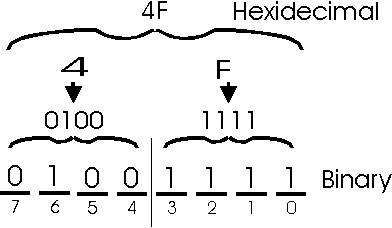
Converting hexadecimal to binary: This is simply the reverse of the above process. For every hexadecimal digit, just write down the 4-bit pattern that represents it. Here is an example which converts hexadecimal number 4F to binary.

Homework Questions

Convert the following binary numbers to octal
1. 100
2. 0
3. 111111
4. 1110111011101
   
   Convert the following binary numbers to hexadecimal
5. 1011
6. 0
7. 11011
8. 1110001011
9. 101100101100
   
   Convert the following octal numbers to binary
10. 35
11. 561
12. 3750
13. 777
14. 0
    
    Convert the following hexadecimal numbers to binary
15. 33
16. 5F
17. F2B
18. C12
19. FF1F