Module 4 Section 2- Floating-point Representation

Just as we use a bit field to represent integers in a computer, we also use a bit field to represent approximations of real numbers.  These are called "floating point" numbers because the binary point is always stored in a normalized position, which could be several places away from where it actually occurs (in other words, the binary point "floats" as needed to maintain normalization). We say floating point numbers are approximations of real numbers because there are an infinite number of reals, and only 2ⁿ possible floating point numbers in an n-bit field. To store a real number, we must find a floating point number that is "close to" or "approximates" the real number. We do this using the techniques we learned in section 1.

Remember that a binary number written in a normalized exponential form has two parts: the mantissa and the exponent. Both of these numbers can be represented individually as integers in computer memory. For example, the number

is actually two numbers which can be represented by the integers 10101 (the mantissa) and 101 (the exponent). We do not need to store the binary point since we know it will always occur to the right of the most significant digit. We say the binary point is implied. So, to store this number we would need 8 bits.

Well, we could store it in 8 bits, but there are still some questions that are unanswered:

• How do we store negative exponents? If we want to store negative expontents, then we probably will need more bits for the exponent, even to store the postive 5 we want to store in this example. (If we only use three bits, this positive 5 might be interpreted as a negative number.)
• How do we store negative numbers? What if this entire number is negative? How do we indicate this?

The second question is easiest: in floating point, we use a sign bit to indicate negative numbers.  This is the same idea we had with sign-magnitude representation for integers. Whereas sign-magnitude doesn't work well for integers, it is the best choice for floating point numbers.

Now, as for the negative exponents, we could choose to use two's complement. In fact, some computers do. However, most implementations use yet another representation for negative numbers to store exponents, called the characteristic or biased exponent. Let's learn what it is before we learn why it is better than two's complement for this task.

Suppose you want to store the exponent e in t bits. First, you compute the characteristic c for e in t bits and store the result. This is done by adding the bias to the exponent. The bias is 2^t-1. Here's the formula:

For example, suppose you want to store the exponent 4 in 6-bit field. The characteristic is 4+2⁵, or 36.  We would actually store the bit pattern for 36 in the 6-bit field, which would be '100100.' Later, if you know the characteristic of a floating point number and wish to determine the exponent, you would subtract the bias 2^(t-1) from it.

Here is a number line for characteristics stored in 4 bits. The exponents being stored are shown across the top.  The characteristics (biased exponents) and their associated bit patterns are shown across the bottom.

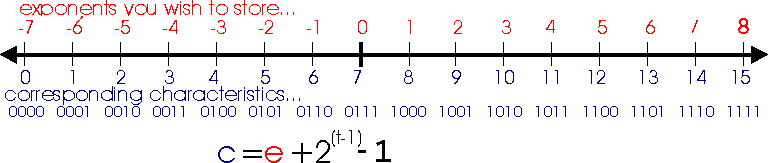
The characteristic convention of storing numbers has a primary advantage over two's compliment. Sorting works. We had not considered sorting with our two's complement representation, but think about it: negative numbers look like very large numbers. When we start manipulating exponents in floating-point, we will want to be able to quickly and easily tell which is the larger of two exponents. Using the biased exponents, this becomes a simply comparing two non-negative numbers.

Now, how to take all of this information and store it in a computer memory? First, we must know how many bits we have in total to work with per value. To be general, let's say we have n total bits to work with. One of the bits (the most significant) will be the sign bit. We split the remaining n-1 bits into two groups. The first group will hold the biased exponent. The second group will hold the mantissa.

Obviously, you have to trade off bits between the exponent and the mantissa. The more bits you give the exponent, the wider the range of numbers (magnitudes) you can represent, but the precision is poorer. In other words, you can represent really big numbers, but the numbers being stored are very rough approximations. If you give more bits to the mantissa, you can improve the precision, but the range is limited. A simple observation about binary numbers in normalized form will allow us to get one more bit of precision without actually adding more bits to the mantissa. For every number except zero, the first significant digit is always a '1'. This leading '1' is never stored, but is always implied. Also, the binary point is not stored, but implied to occur at a certain position, depending on the normalization that has been adopted. The IEEE 754 standard for binary floating-point numbers uses normalized exponential form, which means the binary point is implied to the left of the implied 1.  The IEEE 754 single precision format, shown below, uses 32 bits total, with an 8-bit exponent and 23 bits which represent a 24-bit mantissa (remember the implied 1!).

It is important to realize that the floating-point numbers are approximations, in most cases, of the actual number we wish to store. Most of the time the actual number is truncated or rounded to the nearest floating-point number. The amount of the error increases the further away from zero you go. The number line below shows a typical distribution pattern. The density of floating-point numbers to real numbers decreases the farther away from zero one goes. The 'x' simply indicates that this density halves at regular intervals.

Now let's actually store a floating-point number. To keep things simple, let's choose an 8-bit representation with 1 bit for sign, 3 bits for biased exponent, and 4 bits for mantissa. This format is shown below. The mantissa has an implied '.1', just as the IEEE format does.

Since we have t=3 bits for the exponent, the bias is 2^t-1. That means we'll be adding 4 to every exponent we store. What does the following bit pattern represent if it is interpreted with the above format?

When the bits are interpreted in the appropriate fields, we have:

Let's examine each field separately:

• The sign bit is '0'. This is the easiest one. The entire number is a non-negative number.
• The biased exponent is '110'. The biased exponent is 6. To determine the original exponent, we must subtract the bias, which is 4. The original exponent, therefore, is 6-4, or 2 (which is 10 in binary).
• The mantissa is '1011.' Since there is an implied '.1' before the stored bits, the actual mantissa is .11011

So, we have the following binary number in normal exponential form:

Now, we adjust the binary point by moving it to the right 2 places (as the exponent dictates), and the final number is:

How would you store the following number into our example format?

First, we should remove any insignificant digits. In this case, that means removing the leading zeros:

Next, we move the binary point to the normalized position, and add the exponent. We'll have to move the binary point 3 (11B) places to the left.

Finally, we truncate all digits beyond those which we can actually store. Our mantissa can store the first 5 bits (remember, the .1 is implied).  So now we have:

Now we can determine the contents of the fields in the floating-point representation.

• Since this is a negative number, the sign bit will be '1'.
• The exponent is 3. Adding the bias 4 yields a biased exponent of 7, which is 111B.
• The mantissa is .11110. Since the .1 is implied, we only have to store 1110.

What would happen if you tried to store the number 0.0000000101 in our format? You would realize that the exponent (-7) cannot be stored in our 3-bit exponent. This situation (where we are trying to store a number that is smaller than we can represent) is called underflow. Overflow can also occur, which is when we try to store a number that is too large to be represented.

There are still some questions remaining about floating point format:

• If a '.1' is always implied, then how can we represent the number zero? The answer is that we reserve a special bit pattern to represent zero. The IEEE standard, for example, defines zero to be a sign bit of 0, an exponent of all 0's, and a a stored mantissa of all 0's.
• Are there other special patterns? Yes, the IEEE standard also allows for special bit patterns that represent infinity, negative infinity, Not_a_Number (NaN), and even negative zero (for special numeric systems).

Homework Questions

What is the bias for exponents of the follwing sizes?
1. 7
2. 9
3. 12
4. 15
5. 20
   
   What is the range of exponents that can be represented by exponents of the following sizes?
6. 3
7. 6
8. 11
9. 14
10. 16
    
    Refer to our example format of 8 bits (1 sign, 3 exponent, 4 mantissa). What is the binary number represented by:
11. 01011010
12. 11011011
13. 00001011
14. 11011011
15. 11111111
    
    Store the following binary numbers using our example binary format.  Be sure to note if an overflow or underflow occurs.
16. 01.1011011
17. 0.00101101
18. 1001.0101
19. 1.1000001
20. 0.00001111

Previous Section: Significance
Next Section: Floating-point Operations
Return to Module Index