Chapter Outlines

Ch. 1: Overview and History

Names and Scope

These notes cover Chapter 2, and mentions a few things which your authors cover in Chapter 3. Chapter 3 goes into more detail than we need for this class; you are responsible for Chapter 2, and whatever else is mentioned here.

1. Syntax issues.
   1. Character set.
   2. Blanks
      1. Usually discarded except in string literals.
      2. Separate parts.
      3. Python uses indents for grouping.
   3. Fixed v. free format.
      1. Early languages: one statement per card or line.
      2. Position on the line matters.
      3. Later: ignore lines and white space, terminate with semicolon.
      4. Retro trend: to lines: Python, Ruby.
2. Expressing structure.
   1. Context-Free Grammars / Backus-Naur Form
      1. Substitution rules.

         binaryDigit	→	0 | 1
         unsignedBinaryNumber	→	binaryDigit | binaryDigit unsignedBinaryNumber
         binaryNumber	→	sign unsignedBinaryNumber
         sign	→	+ | −

         1. A grammar has:
            1. Set of productions P
               Each of listed rules is a production.
            2. Set of terminal symbols T
               Symbols like 0 that aren't replaced.
            3. Set of non-terminal symbols N
               Symbols like binaryNumber that are replaced.
            4. One non-terminal is the desginated the start symbol.
         2. A series of replacements to a string of all terminals is a derivation.
         3. The set of all the strings which can be derived from a grammar is the language of the grammar.
      2. BNF notation

         ⟨binaryDigit⟩	::=	0 | 1
         ⟨unsignedBinaryNumber⟩	::=	⟨binaryDigit⟩ | ⟨binaryDigit⟩ ⟨unsignedBinaryNumber⟩
         ⟨binaryNumber⟩	::=	⟨sign⟩ ⟨unsignedBinaryNumber⟩
         ⟨sign⟩	::=	+ | −

      3. Extended notation

         binaryDigit	→	0 | 1
         unsignedBinaryNumber	→	binaryDigit { binaryDigit }
         binaryNumber	→	( + | − ) unsignedBinaryNumber

      4. Imposes structure.
         1. Parse trees.

            expr	→	expr + term | term
            term	→	term * prod | prod
            prod	→	id | const | ( expr )
            id	→	a | b | c
            const	→	1 | 2 | 3

         2. Ambiguity.

            expr	→	expr + expr | expr * expr | ( expr ) | id | const
            id	→	a | b | c
            const	→	1 | 2 | 3

         3. Dangling else problem.

            stmt	→	id := expr
            stmt	→	if expr then stmt
            stmt	→	if expr then stmt else stmt

      5. Left-most and right-most derivations.
      6. ECFG for Tucker and Noonan's Clite Language
   2. Tokens
      1. Grammar has to end somewhere.
      2. Can go to characters; usually end with “tokens”.
         1. Identifiers.
         2. Keywords.
         3. Operators and punctuation.
         4. Literals (constants).
   3. Examples Grammars
      1. Pascal (offsite)
      2. Plain C
      3. Java (offsite)
   4. Abstract syntax.
      1. Throw away the structural tokens: keywords, punctuation.
      2. Collapse single symbol replacements, like expr → term.
      3. Remainder describes the computation.

         expr	=	binary | varref | const
         binary	=	operator op; expr left, right;
         operator	=	+ | *
         varref	=	String id
         const	=	Integer val

      4. Abstract Syntax for for Tucker and Noonan's Clite Language
3. Tokens: Terminals in a language grammar.
   1. Language CFG terminals are not individual characters.
   2. Terminate with “tokens”: identifiers, constants (various types), operators and punctuation.
4. Regular expressions describe tokens.
   1. Characters represent themselves.
   2. Operators * + and |.
   3. Character sets.
   4. Examples (Unix notation)
      1. Identifier (no underscores): [A-Za-z][A-Za-z0-9]*
      2. Optionally-signed integer: [+-]?[0-9]+
      3. Floating-point (no exponential notation): [0-9]+\.[0-9]*|\.[0-9]+
5. Compiling.
   1. Compiling phases.
      
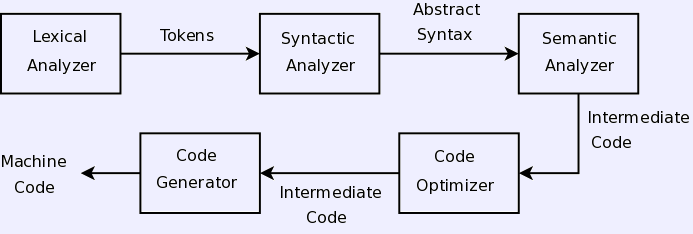
   2. Scanning.
      1. Finite automata implement regular expressions.
      2. Scanner reports a stream of tokens.
      3. Scanner discards white space and comments.
      4. Greedy matching.
   3. Parsing.
      1. Produce the a parse tree from the token stream.
      2. Recursive descent (top-down).
         1. Directly-implemented.
         2. Table-driven.
      3. Bottom-up.

Problems: 2.5, 2.6, 2.7, 2.8 (with Term × Factor), 3.3, 3.10.

Write a CFG to describe Tom's Lisp (there's not much to it).

Some languages have block conditional statements that include their statment lists, like this:

ifstmt	→	if expr then stmtlst [ else stmtlst ] endif
stmtlist	→	{ statement }

Is this ambiguous? Why, or why not?

Construct CFGs for:

• A for-each loop that iterates a variable through a list of expressions. Choose your favorite keywords and syntax.
• Function calls in a language that allows you to omit arguments, like this: f(a, 10, , n + 1 , , 3).

Construct regular expressions for:

• Identifiers which can contain letters and digits, and may even start with a digit, but must contain at least one letter.
• C-style strings which must start and end with double quotes, and may contain double quotes only if preceded by a backwards slash.

Ch. 1: Overview and History

Names and Scope