Syntax is what a program looks like. More formally, which strings of characters form a legal program?

These notes cover Chapter 2, and mentions a few things which your authors cover in Chapter 3. Chapter 3 goes into more detail than we need for this class; you are responsible for Chapter 2, and whatever else is mentioned here.

1. Syntax issues.
   1. Character set.
   2. Blanks
      1. Usually discarded except in string literals.
      2. Separate parts.
      3. Python uses indents for grouping.
   3. Fixed v. free format.
      1. Early languages: one statement per card or line.
      2. Position on the line matters.
      3. Later: ignore lines and white space, terminate with semicolon.
      4. Retro trend back to lines as statements: Python, Ruby, Go.
         1. Statements generally end at the end of a line.
         2. Some syntax to continue.
         3. Frequently continues automatically until parens are balanced.
         4. Semicolon may allow multiple statements on one line.
2. Expressing structure.
   1. Context-Free Grammars / Backus-Naur Form
      1. Substitution rules.

         binaryDigit	→	0|1
         unsignedBinaryNumber	→	binaryDigit|binaryDigitunsignedBinaryNumber
         binaryNumber	→	signunsignedBinaryNumber
         sign	→	+|−

         1. A grammar has:
            1. Set of productions P
               Each of listed rules is a production.
            2. Set of terminal symbols T
               Symbols like 0 that aren't replaced.
            3. Set of non-terminal symbols N
               Symbols like binaryNumber that are replaced.
            4. One non-terminal is the desginated the start symbol.
         2. A series of replacements to a string of all terminals is a derivation.
         3. The set of all the strings which can be derived from a grammar is the language of the grammar.
      2. BNF notation

         binaryDigit	::=	0|1
         unsignedBinaryNumber	::=	binaryDigit|binaryDigitunsignedBinaryNumber
         binaryNumber	::=	signunsignedBinaryNumber
         sign	::=	+|−

      3. Extended notation

         binaryDigit	→	0|1
         unsignedBinaryNumber	→	binaryDigit{binaryDigit
         binaryNumber	→	(+|−)unsignedBinaryNumber

      4. Imposes structure.
         1. Parse trees.

            expr	→	expr+term|term
            term	→	term*prod|prod
            prod	→	id|const|(expr)
            id	→	a|b|c
            const	→	1|2|3

         2. Ambiguity.

            expr	→	expr+expr|expr*expr|(expr)|id|const
            id	→	a|b|c
            const	→	1|2|3

         3. Dangling else problem.

            stmt	→	id:=expr
            stmt	→	ifexprthenstmt
            stmt	→	ifexprthenstmtelsestmt

      5. Left-most and right-most derivations.
      6. CLite EBNF
   2. Tokens
      1. Grammar has to end somewhere.
      2. Can go to characters; usually end with “tokens”.
         1. Identifiers.
         2. Keywords.
         3. Operators and punctuation.
         4. Literals (constants).
   3. Examples Grammars
      1. Pascal (offsite, Felix Colibri)
      2. Plain C
      3. Java (offsite, Oracle)
   4. Abstract syntax.
      1. Throw away the structural tokens: keywords, punctuation.
      2. Collapse single symbol replacements, like expr→term.
      3. Remainder describes the computation.

         expr	=	binary|varref|const
         binary	=	operatorop;exprleft,right;
         operator	=	+|*
         varref	=	Stringid
         const	=	Integerval

      4. Clite abstract syntax.
3. Tokens: Terminals in a language grammar.
   1. Language CFG terminals are not individual characters.
   2. Terminate with “tokens”: identifiers, constants (various types), operators and punctuation.
4. Regular expressions describe tokens.
   1. Characters represent themselves.
   2. Operators * + and |.
   3. Character sets.
   4. Examples (Unix notation)
      1. Identifier (no underscores): [A-Za-z][A-Za-z0-9]*
      2. Optionally-signed integer: [+-]?[0-9]+
      3. Floating-point (no exponential notation): [0-9]+\.[0-9]*|\.[0-9]+
5. Compiling.
   1. Compiling phases.
      
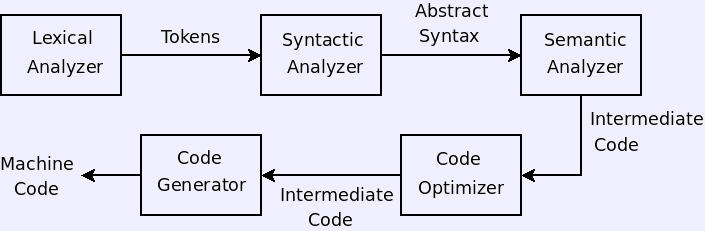
   2. Scanning.
      1. Finite automata implement regular expressions.
      2. Scanner reports a stream of tokens.
      3. Scanner discards white space and comments.
      4. Greedy matching.
   3. Parsing.
      1. Produce the a parse tree from the token stream.
      2. Recursive descent (top-down).
         1. Directly-implemented.
         2. Table-driven.
      3. Bottom-up.

Problems: 2.5, 2.6, 2.7, 2.8 (with Term×Factor), 3.3, 3.10.

Write a CFG to describe Tom's Lisp (there's not much to it).

Some languages have block conditional statements that include their statment lists, like this (EBNF):

ifstmt	→	ifexprthenstmtlst[elsestmtlst]endif
stmtlist	→	{statement}

Is this ambiguous? Why, or why not?

Construct CFGs for:

• A for-each loop that iterates a variable through a list of expressions. Choose your favorite keywords and syntax.
• Function calls in a language that allows you to omit arguments, like this: f(a, 10, , n + 1 , , 3).

Construct regular expressions for:

• Identifiers which can contain letters and digits, and may even start with a digit, but must contain at least one letter.
• C-style strings which must start and end with double quotes, and may contain double quotes only if preceded by a backwards slash.

Derivation Problem Regular Expression Problem