

Process Scheduling

- Intro.
- Policy for deciding which process to move to the running state.
- Traditionally, only one CPU to schedule. Not so much now.
- Properties.
- We view jobs as alternatively running on the CPU or waiting for i/o.
- Periods running the CPU are called bursts. We schedule bursts.
- Jobs with long bursts are called CPU-bound.
- Jobs with few or short bursts are called I/O-bound.
- As CPUs get faster, jobs become more I/O-bound.
- Batch Scheduling Algorithms.
- First-Come First-Served
(FCFS, also sometimes FIFO).
- Shortest Job First (SJF).
- Shortest Remaining Time (SRT). Pre-emptive version of SJF.
- Last two assume job execution is time is known in advance. For
frequently-run batch jobs, this may be true.
- Interactive Scheduling.
- Round-Robin
Quantum 1,
Quantum 4.
- Priority Scheduling/Multiple Queues.
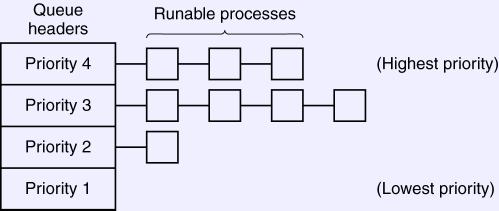
- Let the highest priority job run.
- Move down when a full quantum is used.
- Perhaps move up a job that has been stuck in a low queue a long time.
- May have longer quanta in lower-priority queues to reduce overhead for
CPU-bound jobs.
- Shortest Process Next.
- Same as SJF, using a running average of bursts over time as a predictor.
- Ti is the actual time of the i-th burst.
- Si is the predicted execution time of the i-th burst,
with S0 being a pure guess.
- Sn+1 = aTn+(1−a)Sn,
where 0 ≤ a ≤ 1 is an arbitrary
parameter.
- Larger a favors recent measurements; smaller gives a
longer-term average.
- For a = 1, Sn+1 = Tn: Guess the next burst will
be the same as the last.
- For a = 0.8, Sn+1 = 0.8Tn + 0.16Tn−1 + 0.032Tn−2 + 0.0064Tn−3 + ...
- For a = 0.5, Sn+1 = 0.5Tn + 0.25Tn−1 + 0.125Tn−2 + 0.03125Tn−3 + ...
- For a = 0, Sn+1 = S0.
- Guaranteed Scheduling.
- Give each process an equal portion of the CPU time.
- Keep track of CPU time used by each job.
- For each job, compute a entitled amount of time as the time in
system divided by the number of jobs
- For each job, take the ratio of the actual cpu time over the amount
entitled.
- Run the job with the lowest ratio until it catches up.
- Lottery scheduling.
- Give every job some number of tickets.
- Pick a ticket at random, and run that job.
- Different numbers of tickets give different priorities.
- Does not discriminate (for or against) older jobs.
