The lisp list structure is quite flexible, and can be used to represent any number of things. This file defines Tom's Lisp operations to create and maintain binary search trees of integers inside the list structure. The representation is simple enough. Each node in the tree is a list of three things: The data value at the node, the left subtree, and the right subtree. A tree is either empty, represented by nil, or not empty, represented by a node list, including its subtrees. For instance,
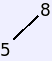This creates the very simple tree at the right. See that the
root is 8, its left child is leaf node 5, and the root has no
right child.
Of course, a complicated tree can be hard to read, but the tree operation file also contains a printer which makes it a bit easier.
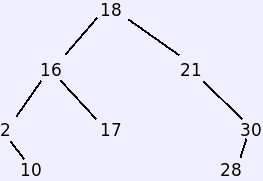The method btree-print outputs the structure in a way that's
at least more tree-like than the basic list representation. Think of it
as printing the tree rotated 90 degrees counter-clockwise so that the root
is on the left. The final nil in the printout is the value of the function.
(Printing is a side-effect.)
The BST file contains these primary functions:
Takes an integer item and a tree tree, and returns a new version of the tree with item added to it.
Takes a list of integers itemlist and a tree tree, and returns a new version of the tree with each member of items added to it, in order left to right.
Takes an integer item and a tree tree and returns a copy of tree with item removed. If tree does not contain item, an unchanged copy of tree is returned. If tree contains multiple copies of item, the highest one is removed.
Prints the tree tree and returns null.
Notice that operations which update the tree always return copies. There is no notion of updating an existing tree in place; just making a new one with changes. This is the nature of Lisp as a purely functional language.
For this assignment, create a file which can be loaded into Tom's Lisp after loading bintree.lsp. You may assume all of its definitions are available to you. Implement the following functions:
Takes an integer item and a BST tree and returns #t if tree contains item, or nil otherwise. Use the standard BST search techniques to perform no more than O(log n) comparisons in a tree of n nodes.
Takes an integer item and a BST tree and returns an integer count of the number of times item occurs in tree. The existing insert method is happy to place multiple copies in a tree, so this really is different from the other method. As the previous, log n behavior is required.
Return a plain Lisp list containing the items in BST tree arranged in in-order (sorted order). Hint: You will probably want to use the built-in append function in the body of your btree-list-in.
Return the maximum value in the tree. If the tree is empty, return nil. Do not use more than O(log n) steps to find the maximum value.
Return a copy of BST tree with its maximum element removed. If tree is empty, return the empty tree. If the maximum element appears more than once, any single copy may be removed.
When your function works, is nicely formatted and documents, submit it using this form.
![[^]](http://sandbox.mc.edu/icons/local//up3.gif){kind=icon}