Replacement
Mississippi College
Computer Science
Dr. Bennet
  1. When a page must be removed from memory to make room for another, this is a replacement.
  2. The rules for deciding which page form a replacement policy. [ Worksheet ]
  3. Page references.
    1. As a program runs, it generates a series of memory references.
    2. The page number parts of these are a series of page references.
    3. The first new page references are placed in unused frames. When they're all full, a replacement algorithm will need to decide which to remove.
  4. Optimal replacement.
    1. Replace the page that will remain unused for the longest time.
    2. Cannot be implemented without knowledge of the future.
    3. Represents the upper limit of any possible algorithm.
  5. Least-Recently Used (LRU).
    1. Replace the page that has remained unused for the longest time.
    2. Best approximation of optimal.
    3. Too expensive to be practical.
      1. Would need to keep all the pages in a linked list.
      2. Update on each memory reference.
      3. (Or something worse.)
  6. The base practical algorithms approximate LRU.
    1. The page table contains two bits manipulated by hardware.
      1. The referenced bit it set whenever the PTE is used.
      2. The modified bit is set whenever the PTE is used for any operation which stores into memory.
    2. The OS can clear these bits.
    3. If the referenced bit is cleared periodically, it means “used recently.”
  7. Not Recently Used
    1. Periodically clears the ref bit. Typically every 20ms.
    2. Pages fall into one four categories based on those bits:
      RMClass
      00Class 0, not referenced, not modified
      01Class 1, not referenced, modified
      10Class 2, referenced, not modified
      11Class 3, referenced and modified
    3. Chooses to a random page from the lowest-numbered non-empty category.
      Can't all be empty, unless there are no pages.
    4. Prefers to remove an clean page since it is cheaper to replace.
  8. FIFO and friends.
    1. First-In, First-Out (FIFO) Algorithm.
      1. Simply remove the page that has been in memory the longest.
      2. Keep the pages in a queue.
      3. This is a terrible algorithm.
    2. FIFO with second-chance. FIFO with this change:
      1. When a page reaches the front of the queue, if its R bit is 0, replace it.
      2. If its R bit is 1, clear the bit, move the page to the end of the queue, and repeat.
    3. Clock algorithm A simpler implementation of second chance.
      1. Keep the pages in a circular list.
        Probably just rotate through the real page numbers using a modular increment.
      2. On a fault, the hand moves and clears referenced pages. It evicts the first un-referenced one found.
  9. Page Aging
    1. Each page is assigned an “age.”
      1. It is a measure of how often the page has been referenced recently.
      2. It is not a time measure.
      3. It's not really anything like an age.
    2. The system updates ages of all pages at some regular period. For each page:
      1. The age is shift right, and the referenced bit is shifted into the left bit position.
      2. The referenced bit is cleared.
    3. The age is larger when
      1. It is used more often (contains more ones).
      2. Was used more recently (one shifted into the left more recently).
      Example
  10. Not Frequently Used (NFU)
    1. Like aging, except the referenced bit is simply added to the age instead of shifted into the left.
      The age is simply a sum of the reference bits over time.
    2. Performs poorly because it treats two references the same regardless of when they occurred.
  11. Working Set
    1. Programs need a certain set of pages.
    2. Working set algorithm is based on keeping an estimate of that set in memory.
    3. Working set.
      1. The working set of size k at time t, given as w(k,t), is the set of pages referred to in the last k memory references at time t.
      2. The time t should be a count of memory references, but usually time is used.
      3. For instance:
        Given the sequence of page references (ending at t at left, with older references to the right):
        10 15 10 12 10 15 27 10 15 27 19 10 15 19 12 15
        Produce the following values:
        w(1,t) = {10}
        w(2,t) through w(3,t) = {10,15}
        w(4,t) through w(6,t) = {10,12,15}
        w(7,t) through w(10,t) = {10,12,15,27}
        w(11,t) through w(17,t) = {10,12,15,19,27}
      4. Increasing function of k:
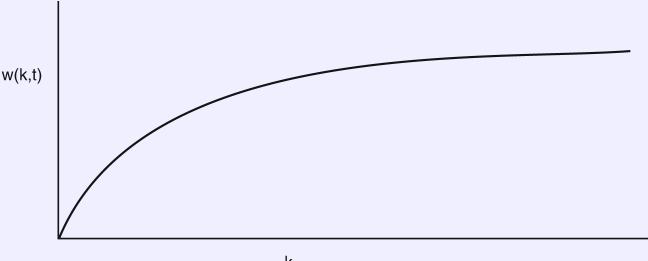
    4. OS Furniture.
      1. Each process has an age, which is just the amount of time it has run.
        1. When the OS moves the process to the running state, record the current clock time as the start time.
        2. When the OS moves the process from the running state, add the difference between the current clock time and the start time to the process age.
      2. Each page has a last-referenced time.
        1. Periodically check each page. If the referenced bit is one, the last-referenced time of the page is set to the age of the process which the page belongs to.
        2. Then clear the ref bit.
      3. Each page has an age, which is simply the current time less the last-referenced time.
    5. Basic procedure
      1. Don't know the optimal k value, so pick one and call it τ. Try to keep w(τ,t) pages in memory for each process.
      2. On a fault, evict a page whose age is greater than τ.
    6. WS-Clock algorithm. On a fault:
      1. Examine the current page. If R=1, clear it and try the next page.
      2. If the page age ≤ τ, try the next page. (Third chance?)
      3. Else (the page age > τ)
        1. If M=0, evict this page. Done.
        2. If M=1, schedule a write, and try the next page. (Not a fourth chance, just house arrest.)
      4. The number of writes scheduled may be limited to a reasonable maximum.
      5. If the hand goes all around and finds not candidate,
        1. If some writes were issued, wait for one to finish, and use that.
        2. Otherwise, just pick one at random.