1. Any data communication system is susceptible to errors.
2. Major error sources
   1. Interference: Unwanted energy enters the system from outside.
   2. Distortion: The shape of the signal is not fully preserved by the system.
      1. Some frequencies may be blocked while others transmitted.
      2. Optical fibers cause waves to disperse.
   3. Attenuation. Energy is lost as the signal travels over distance.
3. How errors present themselves.
   1. Single-bit error: An isolated bit is inverted.
      Often due to short interference events.
   2. Burst errors: Multiple contiguous bits are inverted
      Often due to longer-term interference.
   3. Erasure/ambiguity: a portion of the signal is no longer identifiable as one or zero.
4. Approaches.
   1. Automatic Repeat Request (ARQ): The receiver detects the error and requests a resend.
   2. Forward Error Correction (FEC): The receiver detects and fixes the error.
   3. Collectively, channel coding.
5. Key Idea: Redundant information.
   1. Detection and correction involve sending extra (redundant) information along with the message contents itself.
   2. The redundant information is computed from the message by the sender, and verified by the receiver.
   3. Simplest form.
      1. For detection (ARQ): Send two copies of everything. If they agree, assume the transmission is correct. Otherwise, request re-transmission.
      2. For correction (FEC): Send three copies of everything.
         1. If all agree, no error.
         2. If two out of three agree, assume that version is correct.
         3. If all three differ, either fail for fall back to ARQ.
   4. Practical systems use less redundant information than that simplest form.
   5. Limitations.
      1. Systems assume that transmission works correctly most of the time.
      2. Failure to detect, or faulty correction are always possible, but should be very unlikely.
6. Code types
   1. Block Error Code: Information is divided into blocks. Redundant info is attached to each block, and is a function of it.
      1. If k bits of payload data require r bits of redundancy, the system is an (n,k) encoding scheme, where n=k+r.
      2. A measure of the scheme's overhead is the code rate:
         R=

         k

         
         

         n
   2. Convolutional: Message is treated as a bit stream, and the redundant information at any point is a function of all before. No fixed-size blocks.
7. Single-bit parity: Simple block error detecting code.
   1. Operation.
      1. Typically, a block is one byte. Each block is extended by one redundant bit.
      2. For even parity: The number of ones in the nine-bit group should be even; for odd parity, odd.
      3. Sender computes the correct bit, receiver verifies it. Incorrect parity indicates a bit error.

         Original Data	With Even Parity	With Odd Parity
         00000000	000000000	000000001
         10001110	100011100	100011101
         00100011	001000111	001000110
         11111111	111111110	111111111
         01100010	011000101	011000100

   2. This is a (9,8) coding scheme.
   3. How well can it work?
      1. Obviously, will only catch errors where the number of incorrect bits is odd.
      2. Assume that the probability of a bit error, p is small.
      3. Assume that bit errors are independent (that is, no burst errors).
      4. Then
         1. The probability of an error in exactly one bit (detected) is p(1−p)8.
         2. The probability of an error in exactly two bits (undetected) is p2(1−p)7.
      5. If the assumptions are true, the most-likely detected error is much more likely than the most-likely undetected error. In fact, any error beyond one bit is very unlikely.
      6. The assumptions need not be true.
8. The Hamming distance between two bit strings is the number of bits which must change to get from one to the other.

   d(1010,0100)=3	d(0001,0000)=1	d(1001,0110)=4
   d(1100,1110)=1	d(1101,1010)=3	d(0011,0110)=2

9. Codebook
   1. For an (n,k) coding scheme, there are 2n possible messages, of which 2k are valid.
   2. The set of valid ones is called the codebook.
   3. A change to an entry in the codebook may produce another codebook entry, or an invalid bit pattern.
   4. Ideally, any change to a codebook entry would produce an invalid one.
      Obviously, this is impossible.
   5. For single-bit parity on a byte, change any one bit produces an invalid, two bits produce another codebook entry.
   6. The minimum Hamming distance between any two code entries is denoted dmin. Measure of the scheme's strength.
   7. For parity, dmin=2.
   8. Errors of more than dmin−1 bits may go undetected.

   1	0	1	1	1
   0	0	1	0	1
   1	0	1	0	0
   0	0	1	1	0

10. Row And Column (RAC) parity: Block error correcting.
    1. Arrange the data as a two-dimensional array.
    2. Compute a parity bit for each row and each column. (And another for the whole thing.)
    3. The example at right is a (20,12) scheme which arranges the payload arbitrarily in a 3x4 grid.
    4. The position of a single-bit error can be determined by which row and column shows a parity error.

       1	0	1	1	1
       0	1	1	0	1
       1	0	1	0	0
       0	0	1	1	0

    5. The error can be corrected by simply inverting the indicated bit.
    6. RAC can correct single-bit errors, and detect (but not correct) any error involving a larger odd number of bits.
    7. It can also detect errors with small even numbers of bits.
11. Hamming codes: Block error-correcting.
    1. Number bit positions in the transmission starting at 1 (instead of zero for once).
    2. Each position indexed by a power of two is a parity bit; other positions are payload data.
    3. Each parity bit is computed over some of the data bits based on the position values expressed in binary:
       1. Positions which are powers of two contain parity bits.
       2. Other positions contain data bits. A data bit contributes to each parity bit corresponding to the place value of a one in its position number.
       3. For instance
          1. The bit in position 13 is included in the parity bits at 8, 4 and 1.
          2. The parity bit in position 1 is computed over all the data bits in odd positions, since they have ones in their ones place.
          3. The parity bit in position four is computed over data positions, 5–7, 12–15, 20–23, etc., up to the maximum number of data positions. These are the locations which have ones in their fours place.
       4. Since data bits are not powers of two, every one is covered by at least two parity bits.
       5. Every parity bit covers a different set of data bits.
       6. For a single-bit error, the receiver simply totals the positions of mismatching parity bits to find the position of of the error bit.
    4. A (20,15) example.
       1. Here is a correct transmission. The parity positions are indicated. If you hover over a parity bit, the figure shows which data bits it covers. If you hover over a data bit, the figure shows which parity bits cover it.

          1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
          0	1	1	0	0	1	1	0	1	0	0	1	1	0	1	1	1	1	0	1

       2. Suppose one of the data bits is transmitted incorrectly. The receiver would see something like this:

          1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
          0	1	1	0	0	1	1	0	1	1	0	1	1	0	1	1	1	1	0	1

          The parity bits that cover data bit 10 are 2 and 8, so they detect that error, and together identify the incorrect bit.
       3. Here's another:

          1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
          0	1	1	0	0	1	1	0	1	0	0	1	0	0	1	1	1	1	0	1

       4. If the error is a parity bit, it will be the only parity bit showing the error, and will denote itself.
12. Internet Checksum: Error detecting.
    1. A checksum is a value computed over the message contents. It is appended to the transmission by the sender, and checked by the receiver.
    2. The Internet checksum is a 16-bit number computed over the contents of an Internet datagram:
       1. Break the message into 16-bit units; pad at the end with zeros if needed.
       2. Add the 16-bit units. Any carry-out past the 16-bit size is added in as well.
       3. Invert the sum.
       4. If the result is zero, substitute all ones (65535 decimal).
    3. Use
       1. The sender computes the checksum, and places it in the header.
       2. The receiver verifies it by computing the checksum over both the message and the checksum sent. Zero indicates a correct result.
       3. The sender may send a checksum value of zero to disable the checksum mechanism. The receiver assumes the message is correct.
    4. Example.
13. Cyclic Redundancy Codes: Error detecting.
    1. Like a checksum, a function of the data appended by the sender and checked by the receiver.
    2. Used in high-speed networks, such as Ethernet.
       
    3. Properties
       1. Can operate on variable-length data (as a checksum can).
       2. Excellent error detection ability.
       3. Fast hardware implementation.
    4. The computation can be represented in several ways.
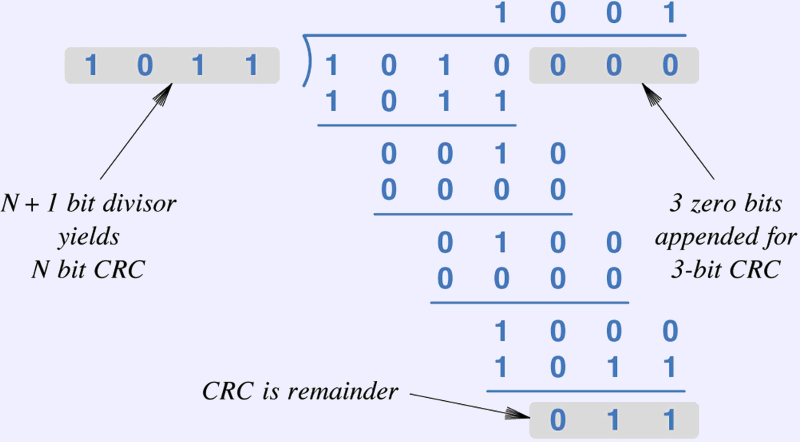
       1. The remainder of an odd sort of binary division, where subtraction is replaced by xor (no borrowing).
          1. The divisor can be “subtracted” when the result has a zero in the high bit.
          2. Divide the message by a some chosen constant.
       2. The division of one polynomial by another.
          1. The coefficients are the bits, so all are 1 or 0.
          2. The example at right (1011 into 1010000) is x3+x+1 divided into x6+x4.
          3. The divisor is called the generator polynomial
          4. Better generators are those divisible only by themselves and 1.
          5. Generator with more than one non-zero coefficient can detect all single-bit errors.
       3. High-speed hardware mechanism.
          1. Hardware for the 1011 divisor
             
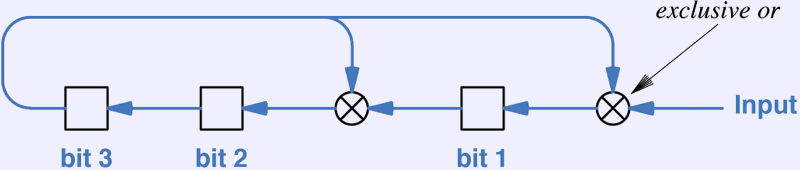
          2. Shift the message in one bit at a time.
             1. Follow the message with zeros the length of the CRC to compute a new CRC.
             2. Follow the message with a received CRC to test it. Will produce zero if correct.
          3. Shifting and XOR are cheap and fast.
14. Methods, again.
    1. FEC can use methods such as RAC or Hamming codes that allow for correction.
    2. ARQ can use either, but using a correcting code for just ARQ is wasteful. Probably use a detecting scheme like checksum or CRC (or possibly simple parity).
    3. An FEC system can also use ARQ as a backup when there are too many errors to correct.